I gave this talk on February 04, 2022 in the analysis seminar of Sylvie Paycha of University of Potsdam, which happened online on zoom.

Abstract:

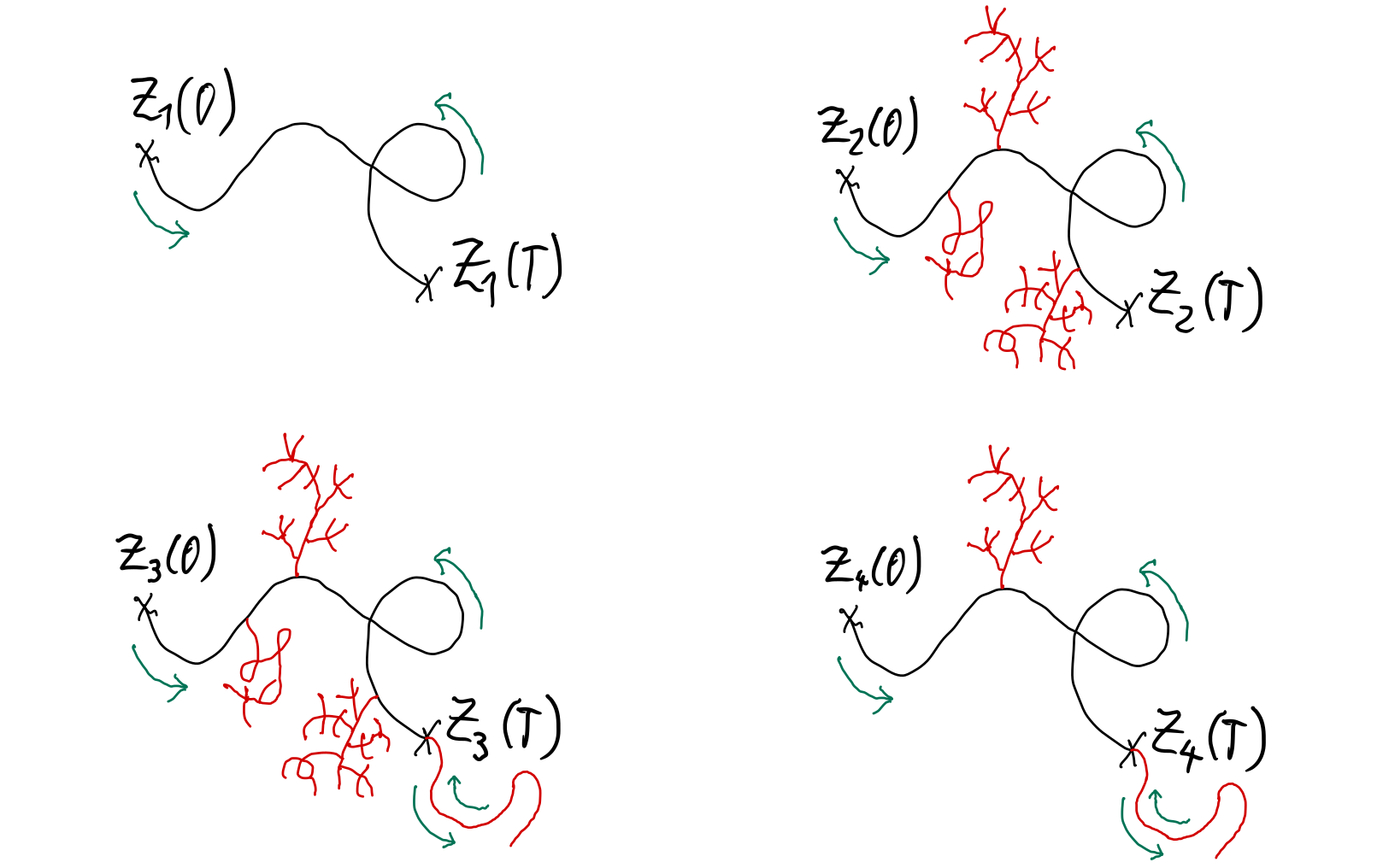
The aim of our project is to give a definite answer to the question posed (in its earliest form) by Chen some 65 years ago, whether or not the signature, i.e. the full time increment footprint in the group-like elements, characterizes the path. We intend to show that the signature uniquely characterizes all reduced rough paths if and only if the primitive elements are free as a Lie algebra.

Our study is carried out in the general setting of finite p-variation rough paths living in the group-like elements of a connected graded cocommutative Hopf algebra of finite type (cgccft Hopf algebra). Using the notion of tree-like equivalence of continuous paths in a metric space originally introduced in 2005, which this talk will present both via visiual examples and rigorously, we state the following conjecture: For a cgccft Hopf algebra, there exists a p>1 and two finite p-variation rough paths which share a common signature while not being tree-like equivalent, if and only if the Lie algebra of primitive elements of the Hopf algebra is NOT a free Lie algebra over a Lie generating subset.

We will discuss how to prove one direction of the statement, and argue how a highly interesting conjecture about the classical iterated-integral signature living in the tensor algebra would imply the other direction if true.

The talk also contains a short excursion into the theory of smooth rough paths, and if time permits, we may briefly touch the connection of the uniqueness statement with the problem of introducing a notion of area between two arbitrary rough path components.

Find the slides here.